Renderosity Forums / Poser - OFFICIAL
Welcome to the Poser - OFFICIAL Forum
Forum Coordinators: RedPhantom
Poser - OFFICIAL F.A.Q (Last Updated: 2024 Dec 02 5:01 am)
Subject: wave without wave-deformer (part 2)

Sure.
I also added another node Math_Functions_11 to
change the phase of the sin. Just enter something
in value_2
By the way, the renderer seems to have an error.
In the middle of the plane there is always this little
tip, no matter how the phase is.
Do you think I should report this to CuriousLabs?
Ernst
I haven't checked all the way through the shader, but I think that the "tip" at the center is a divide-by-zero effect in the Math_Function_9 node when both the u and v coordinates have values 0.5 where the output from the sqrt (Math_Function_5) is zero. Mathematically, you should test for this value and use the identity sin(x)/x -> 1.0. Bill
The tip looks normal to me the wave needs to start somewhere, if you use cos, and start from zero, it should look ok. (You need to rotate turn for sin to start smooth) I recommend using 6.28319 for value 1 in all the trig nodes (sin, cos, tan) this way it will cycle at 1. And I adjust the wave count, on the node before (an add or subtract) (you can also animate the wave from value 2 of this node by attaching the frame number) (node 11). Just to clarify nodes 6 and 7 are the center. Node 5 is the Radius, and node 2 is the Radius squared (I use one or both of these for my dampers). And I am not sure, but I think a multiply might be faster than a POW with value 2 = 2. (When you animate three of these together, and then ray trace through them, all the clock cycles count) Hope this helps, Gary

Well, it is not. But I did try a divide by zero on purpose
and Poser did not crash!
The wave-shader represents the following formula:
sin(40 * r) / sqr(r+1)
r (the radius) is the value of Math_Function_5.
It goes from 0 to 1. So, r+1 goes from 1 to 2.
But, as mentioned above, even without that shift
Poser doesn't crash, but renders the above picture.
The hole in the center is really a result of a div by 0.
Ernst
Minimum displacement bounds are a rendering setting that allows the render to account for displacements that cross the boundaries between render buckets, although trying to account for a (possibly near) infinite displacement may not be worth the trouble. You're right about the formula, the additional bias does eliminate the possibility of divide-by-zero problems. On the other hand, it does occur to me that any sinusoidal function (or cosines for that matter) would inherently suffer from discontinuities at a radial center. If you take any cross-section of the curve through the radius, it's obvious that, except when the phase is other than +/-PI/2 (?), there is going to be a sharp peak or trough at the origin with the cross section reflected on both sides. This may be a lot more apparent with displacement, since the accuracy of the sampling is always a pixel or less, than with other (geometrical deformation) techniques where there is an element of mesh smoothing between sample (vertex) points. It may be that you need to add an additional smoothing function to compensate for the discontinuity at the center. Bill


But look: Math_Functions_9 is directly connected to
the displacement. M_F_9 is smooth, the preview and the
final render are not.
M_F_11 (not shown here) can change the phase of the sin.
But this tip remains always, no matter which value I enter
there.
Ernst
If you change the sin to cos and set the offset to zero, the render will look right, and the preview will have the tip (it does look backwards to me too). If that is not an option try the value .03927 as the offset. The 40 multiplier in the sin node makes that calculation tuff. (I already recommended changing it and using node 11 for the wave count). Hope this helps

Privacy Notice
This site uses cookies to deliver the best experience. Our own cookies make user accounts and other features possible. Third-party cookies are used to display relevant ads and to analyze how Renderosity is used. By using our site, you acknowledge that you have read and understood our Terms of Service, including our Cookie Policy and our Privacy Policy.







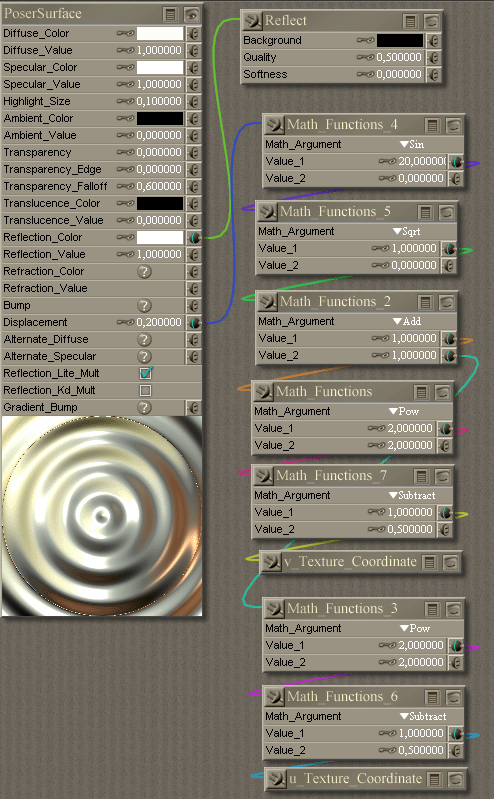
You can use a shader which is the representation of the following expression:sin(20* sqrt(sqr(2u - 1) + sqr(2v - 1)))
If you want more ripples you can increase the 20 to
a higher value.
This wave, however, is not perfect since its amplitude
remains constant with increasing distance wereas a real
wave decreases.
I hope you can use it for something usefull.
Ernst