Renderosity Forums / Poser - OFFICIAL
Welcome to the Poser - OFFICIAL Forum
Forum Coordinators: RedPhantom
Poser - OFFICIAL F.A.Q (Last Updated: 2025 Jan 22 9:27 pm)
Subject: Loop-making script
Quote - I'm not sure what you mean, by the droop amount.
I think markschum's idea was to create a horizontal chain that drooped in the middle due to is own weight. He also said:
Quote - the problem with chains is that the links overlap, so the endpoints are sort of between the two ends. It complicates the joints a lot.
I know what he means, and I think you will see too if you look at my chain figure in Poser. The ideal place for the origin for xrot is not the ideal place in respect to zrot. That means you have to make a compromise and put it half way in-between. That leads to the ends of the links not matching up correctly when the chain is bent. For a slight droop it is not noticeable, but if you were to wrap it round a small circumference like an ankle, it would be noticeable, see my last image.
Ooh! Excellent! This is perfect, Les! Thank you! :woot: This is exactly the kind of information that should help in trying to set up any kind of automatic chain-building feature.
It sounds like you may want the dual joint center ERC setup that was developed by VK several years ago. Complicated stuff, but it could put the joint in two places at once, IIRC.
Maybe I should read those threads again. Didn't understand a bit of them, at the time. :lol: I might grasp at least some of it, now. :unsure:
If a template chain .cr2 could be developed, using the VTK methods, a Python script could hypothetically apply that without too much difficulty. Assuming the programmer can figure out what's happening. :lol:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
I really meant specifying two end points and a value for the lowest point of the chain. It becomes a problem in solving for a parabola using 3 known points.
actually building a chain is not too complex because you can build it in a straight line along an axis, so only a distance from the start needs to be calculated.
I should have put up a picture to illustrate the chain joint issue. I know a few people have tried extra bones between links but I could never get that to work.
If you parameterise the dimensions of a single link properly, it's not hard to work out the correct spacing.
The minimum set is :-
- Curved section radius
- Straight section length
- Radius of the link
Attached is a short segement (4 links), the interesting rotation of an individual link is about the x axis, IIRC.
Okay, I understand now. :lol: I'm slow. Thank you both for explaining! :thumbupboth:
I think building a straight chain is the right thing, particularly if a .cr2 is going to be generated. And building it along Z does seem to make the most sense. Working with parabolas is beyond what I was even contemplating. :lol:
Quote - The minimum set is :-
- Curved section radius
- Straight section length
- Radius of the link
Looking at the image Les posted, I'd assumed I could work out the proper spacing and origin/endpoint placement using only the length of each link and the "Thickness" value. Calculating the proper offsets from that seems possible. Am I under-thinking things again? :lol:
I'll check out all of the examples. Thank you!
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - Catenery ? , darn parabola was hard enough :( maybe catenery will be easier ? ya right .. :)
Oh, aye. :lol:
Thanks for all the help, guys. I'm starting work on this.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
This also adds the "bug" that Les seemed to like, as an option. Run the stacking option with a negative value for the "Stack loops" parameter, and it will build the loop stack within the plane, rather than against the plane.
I think I'm going to be putting the chain-building into a separate script, so I wanted to get this update out before I switch gears and forget. :lol:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
I wanted to find out more about this catenary business, so I Googled and found some Python code. The attached script implements the code at the above link for a quick test, within Poser. The catenary code looks quite simple. Could Cage have written something like this, himself? :lol: :lol: No.
Really, no. :lol:
But the basics seem straightforward. It seems like the real problem with applying the catenary for chain-sag would be getting the angles properly. :unsure:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
*It seems like the real problem with applying the catenary for chain-sag would be getting the angles properly
Yes, you can calculate a position along the curve and calculate the tangent at that point to position links. I had a script for Truespace 4 that made chains but the code was very complex and I lost it in a disk crash a long time ago. *
Cage, I'll have a look at VK's stuff when I can find a bit of time. I may be wrong, but from memory in that thread VK was talking about animating the joint center, changing it over time, the chain link problem is not an animation problem, it requires two different joint centers - at the same time! Anyway I think that's what it was about, but I'll take another look.
markschum said, quote: "I know a few people have tried extra bones between links but I could never get that to work."
I think that is the most promising path to a solution, 'ghost actors' as I call them. Perhaps I am missing something, but in my imagination it would not be hard to implement in principle. In practice it would require a lot of work, too much for it to be an attractive proposition to do it by hand for anything beyond a two or three links, but if we are talking a python implementation a two or three link example should be enough.
I must strongly disagree with the position of the origin as suggested in nruddock's diagram. It will be the best position for one rotation, but the worst for the other. I'll make a diagram of my own to explain why. I believe that the best place for the origin is where the two inner surfaces of the links meet, as per my earlier diagram. However if combined with markschum's idea of extra bones (ghost actors), then nruddock's position does become important as the foci of one rotation, as we could then use two joint centers for each link and have each at its optimal location.
I will try building a short chain with ghost actors, in the hope that you can do a python implementation to do longer chains.
I think pitting the chain-building into a separate script, is a good idea.
I would still like to send you my chain, as I think the problems would be easier to understand if you had a working example. However I don't know where to send it to.

Hmm. Pretty sure this is completely wrong, but this is what I get when I try to apply my vague understanding of the above idea. :unsure: :lol: Actually, I'm surprised it turns out that well. It ends up just being the tangent of the X intervals applied to place the boxes for the cantenary curve. The angles are increasingly off as the curve grows steeper.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - Cage, I'll have a look at VK's stuff when I can find a bit of time. I may be wrong, but from memory in that thread VK was talking about animating the joint center, changing it over time, the chain link problem is not an animation problem, it requires two different joint centers - at the same time! Anyway I think that's what it was about, but I'll take another look.
markschum said, quote: "I know a few people have tried extra bones between links but I could never get that to work."
I think that is the most promising path to a solution, 'ghost actors' as I call them. Perhaps I am missing something, but in my imagination it would not be hard to implement in principle. In practice it would require a lot of work, too much for it to be an attractive proposition to do it by hand for anything beyond a two or three links, but if we are talking a python implementation a two or three link example should be enough.
I must strongly disagree with the position of the origin as suggested in nruddock's diagram. It will be the best position for one rotation, but the worst for the other. I'll make a diagram of my own to explain why. I believe that the best place for the origin is where the two inner surfaces of the links meet, as per my earlier diagram. However if combined with markschum's idea of extra bones (ghost actors), then nruddock's position does become important as the foci of one rotation, as we could then use two joint centers for each link and have each at its optimal location.
I will try building a short chain with ghost actors, in the hope that you can do a python implementation to do longer chains.
I think pitting the chain-building into a separate script, is a good idea.
I would still like to send you my chain, as I think the problems would be easier to understand if you had a working example. However I don't know where to send it to.
I was under the impression that the chain nruddock posted has had the VK method applied to it. There are extra Z translation entries for the link actors, each one ERC-linked in ways that are as-yet mysterious to me. :lol: :unsure:
The script should be able to generate a chain based only on numeric inputs for the link-shaping and chain length. I've applied your two cylinders-looping method internally. The radius of the circles can be set, as well as the thickness of the link and the length of the link. So it pretty definitely belongs in a separate script, because it's no longer doing the same things. It's applying the main loop-building function in a new way.
I'll PM you with my e-mail. :thumbupboth: Thanks for your help!
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - I was under the impression that the chain nruddock posted has had the VK method applied to it. There are extra Z translation entries for the link actors, each one ERC-linked in ways that are as-yet mysterious to me.
I had not gotten round to downloading nruddock's file when I posted my last message, and did not realize he meant to use that origin in conjunction with ERC. It is a very neat solution. ![]()
Quote - There are extra Z translation entries for the link actors, each one ERC-linked in ways that are as-yet mysterious to me. :lol: :unsure:
The extra translations change the centre of rotation for one of the axes so that the link track the inside of the end of the previous link (I got the idea from VK's stuff).

Well, VK's method for moving the origin is not based on ERC, and does not need ERC to work. It just relies on two translate channels for each rot channel that needs its origin moved, a translate channel (lets call it B) after the rot channel determines how far the origin is to be moved, and another translate channel (lets call it A) before the rot channel contains the inverse value and thus restores the origin.
I think it is good news that ERC is not needed, because as I understand it there are problems adding ERC slaving via Python.
Nruddock's chain figure showed the way, but it has a glitch, see image above. So I made a new version of my chain that uses the VK method to adjust the origins. It has two extra channels per actor and no ERC. I'll send you a copy.
Thanks, everyone, for all of the input on this! :thumbupboth: There are many, many things that I'd never considered, when it comes to chains. :lol:
I think the script will be generating .cr2 and .obj files for the chain, then loading the saved .cr2. ERC, extra channels, and ghost actors (whatever ends up being best) shouldn't a problem with Python, if the figure is generated this way, and chain links can also be grouped as they're added to the .obj text before it's written out.
I think the script should be able to build a chain along any of the cardinal axes, in the positive or negative direction. I'm also wondering whether the position of the root actor for the chain should be able to be varied, placing it at either end of the chain, or in the middle. I could imagine different potential benefits to any of these setups, but I'm not sure I'm able to consider all of the important factors involved in the design of such a figure. Is there actually a "best" way to build a chain figure in Poser, in terms of orientation and figure hierarchy?
I'll start putting the geometry-building part of the script together, then work on the figure-build portion as an optimal setup is worked out.
Thanks again! :woot:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - I think the script will be generating .cr2 and .obj files for the chain ... shouldn't [be] a problem with Python
You're right, it isn't a problem.
One thing to think about is that if you're generating the chain in place, does it actually need to be a figure ?
A chain figure is handy for lengths lying around, i.e. not hanging between two points for which you might as well just have a prop (and regenerate if the end points move).
nruddock, quote: "One thing to think about is that if you're generating the chain in place, does it actually need to be a figure ?"
I'm sure both types have their strengths and weaknesses. I'd like to have both (always was greedy), but given the either/or choice, I'd much rather have a figure. Easier to play around and experiment with I think. And don't forget the poor old animators. ![]()
Quote - A chain figure is handy for lengths lying around, i.e. not hanging between two points for which you might as well just have a prop (and regenerate if the end points move).
If you have any pointers for deriving the proper angles for positions along the catenary curve, I can think about trying to approach the hanging-between-two-points problem. I explored the catenary problem yesterday and found some code which can give me the point set, but I'm not convinced I have the angles. I posted an image last night of colored blocks in a catenary curve, but the rotations I derived from my interpretation of markschum's advice seem almost certainly incorrect.
Can you suggest how I can get the proper angles, given the plot points of the curve? I'm afraid my formal math training is limited and I'm pressing against the edges of my knowledge, here. :lol:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - I'm sure both types have their strengths and weaknesses. I'd like to have both (always was greedy), but given the either/or choice, I'd much rather have a figure. Easier to play around and experiment with I think. And don't forget the poor old animators.
I think a figure will be more versatile, myself, particularly if I don't have the necessary math at hand to generate a correctly-hanging prop. If a figure is in use, various methods can be used to pose the chain in a way that at least sort of resembles a mathematically-correct catenary curve.
A script could be written which could pose a chain to place its two endpoints in desired locations while trying to approximate the proper hanging curve, theoretically.
A figure can always be posed to suit, then exported to create a static prop, as well.
Hmm.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Attached Link: http://www.euclideanspace.com/maths/algebra/vectors/angleBetween/index.htm
> Quote - Can you suggest how I can get the proper angles, given the plot points of the curve? I'm afraid my formal math training is limited and I'm pressing against the edges of my knowledge, here. :lol:The simplest way to think of it is that you want to rotate each link onto the curve (starting with the first and working along the chain).
The math for this is quite simple (because again you start with things aligned to the primary axes) and so you're effectively working in 2 dimensions when calculating the required angle between the current link and the target segment of the curve (you need to take notice of the signs, especially once you reach the lowest point).
ISTR that this is why my chain is rigged as it is because it was never intended for general posing, but only to make fitting it to a catenary easy.
Useful reference ->http://www.j3d.org/matrix_faq/matrfaq_latest.html
Vector math -> http://chortle.ccsu.edu/VectorLessons/vectorIndex.html
Picking a convenient set of axes (i.e. frame of reference) is always a good first step as it simplifies things as it's much easier to work with tihngs aligned to the primrary (possibly orthognal) axes and then rotate to match the "real world" axes at the very end than it is to work with arbitary orientation throughout.
You should get into the habit of looking for such a convenient FoR as the first step in a geometry problem.
Thanks, nruddock! That confirms what I know, so hopefully I should be able to try to proceed with the matter. :laugh:
Quote - You should get into the habit of looking for such a convenient FoR as the first step in a geometry problem.
That's actually something I've been learning, with this loop script. Good advice. Thank you. :thumbupboth:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.

Now I just need to apply them to chains. :lol:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Would it be possible, before you get too far into it, to also have the ability to create straight chains of arbitrary length? That way, this script could be used not only for loop chains, but also in conjunction with Ockham's Draw-a-cord script for more complex chain poses.

Yes, absolutely. That's my current plan. :thumbupboth:
The user will be able to define the number of links in the chain, the default axis on which the figure geometry is built, and the size, shape, and style of the links.
The attached shows my test of different link-length settings. The thickness and geometry resolution (sections and slices of the loop) will also be settable, as with the loop-making script, but I don't have an image to illustrate that.
I think a separate script (another one :lol:) should be able to either pose an existing chain in a proper catenary or create a static prop in that pose.
I didn't even know about Draw-a-cord! That's great! :laugh: :thumbupboth:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Which end is the start is just a matter of rotating the chain once its in the scene. I would not complicate matters by trying ro build from either end.
PLEASE PLEASE but some basic erc for bend into the chain. A master fial that will bend all segments equally.
To build a draped chain between two given endpoints consider simplifying by rotating the endpoints parrallel to the axis and then translating it , then build the chain along the axis, and then reverse the translate and rotate back into place . That makes calculating the chain much easier. Its what nruddock was saying about terms of reference.
Quote - Which end is the start is just a matter of rotating the chain once its in the scene. I would not complicate matters by trying ro build from either end.
PLEASE PLEASE but some basic erc for bend into the chain. A master fial that will bend all segments equally.
To build a draped chain between two given endpoints consider simplifying by rotating the endpoints parrallel to the axis and then translating it , then build the chain along the axis, and then reverse the translate and rotate back into place . That makes calculating the chain much easier. Its what nruddock was saying about terms of reference.
You mean, don't bother with an option to build a chain from -z forwards as well as +z backwards? I think I'm interested in the idea mainly because I'm curious about how different hierarchies for a chain might make some difference in how usable it is as a figure. :unsure: Hmm.
Once I get to the .cr2 portion, I'll dig up the EasyPose figures I've made by hand in the past and see what I can do about adding some EasyPose ERC to the chains. Or do you mean I should add the catenary draping as ERC? I think that would be beyond my skills at this point. :lol: If someone wants to work out a donor .cr2 that has catenary ERC in place, I'll happily use the donor to add the feature to chains made by the script.
It's excellent advice, about the frame of reference. :laugh: I've ended up relying on exactly that sort of thing in the new intersection validation process for the loop-making script. I suspect I still have a lot to learn in that area, as I'm still fairly new to using matrices.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - I just meant a simple erc dial for overall bends to the chain rather than posing link by link.
Yes, that should be easy enough. :thumbupboth: Trying to understand how to write a cosh() function using ERC dials, however... not easy. :lol:
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.

You might like to take a look at "Shackles and chains colelction for Poser" by Zark, at sharecg. It contains a "cartenoid99.py" to pose the chain. Note that the obj is missing for the 57 link chain, but the 99 link chain is OK.
Quote -
You might like to take a look at "Shackles and chains colelction for Poser" by Zark, at sharecg. It contains a "cartenoid99.py" to pose the chain. Note that the obj is missing for the 57 link chain, but the 99 link chain is OK.
Huh. Looks like sharecg is broken right now. I'll try again later. Sounds interesting. :laugh:
Quote - Seriously why do that, just use a script to set the angles
I'm planning to use the script, rather than try to write ERC. If someone wanted to work out the ERC, however, I'd happily add it.
It does occur to me that the catenary handling I have now will work if the two ends are at the same height. I'm not sure how to adapt it to handle the ends at the different heights? Hmm. How does the math differ? Is it the same curve in both types of situations, and if the end-heights differ, you just enter and/or leave the curve at different points? I'm afraid all of this is new to me. :lol: I set out to make loops, and didn't expect to end up dealing with certain complexities of chains. :lol:
Edit: Sharecg is back.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
for parabolas the general form of the equation y = ax^2 + bx + c can be solved for 3 points and a matrix used to solve for a,b,c. with those you can solve for the vertex, or just use a range of x in the equation for the start and end points of the chain.
For the hyperbolic cosine I have no idea, but I would expect it to be similar.
Quote - for parabolas the general form of the equation y = ax^2 + bx + c can be solved for 3 points and a matrix used to solve for a,b,c. with those you can solve for the vertex, or just use a range of x in the equation for the start and end points of the chain.
For the hyperbolic cosine I have no idea, but I would expect it to be similar.
Umm. :unsure: Okay. :lol:
My apologies, but I think your math skills are so far beyond mine that I'm not quite sure what you've just said.  Can you provide a URL which could explain more fully, or a search term I could use to use Google to locate such a URL?
Can you provide a URL which could explain more fully, or a search term I could use to use Google to locate such a URL?
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Quote - For the hyperbolic cosine I have no idea, but I would expect it to be similar.
The problem for a Catenary {y = a cosh(x / a)} is that it's easy to find a for a given length of chain when the end points are the same height, if they are at different heights you have a second unknown, where the lowest point of the chain is relative to the ends (in the equal height case this is in the middle and is a special case).
sorry cage , my maths is just as bad as yours :)
I found some good explanations on the internet for solving the formula for a parabola if you have 3 points on it. so if you have (-4,4)(0,1) (3,2) as points you can get the values for y = ax^2 + bx + c (general formula for a parabola) values a.b.c and then calculate
for x = -4 to 3 step 0.5
y = etc
next x and create the curve. (a bit more complex to calculate he exact positions and angles of each link but can be done )
you get three equations which can be solved by an inverse matrix multiplication :scared:
which some kind mathematician did http://stackoverflow.com/questions/717762/how-to-calculate-the-vertex-of-a-parabola-given-three-points
<pre class="prettyprint">
<span class="pln">denom </span><span class="pun">=</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x1 </span><span class="pun">-</span><span class="pln"> x2</span><span class="pun">)(</span><span class="pln">x1 </span><span class="pun">-</span><span class="pln"> x3</span><span class="pun">)(</span><span class="pln">x2 </span><span class="pun">-</span><span class="pln"> x3</span><span class="pun">)</span><span class="pln"><br></br>A </span><span class="pun">=</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x3 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y2 </span><span class="pun">-</span><span class="pln"> y1</span><span class="pun">)</span><span class="pln"> </span><span class="pun">+</span><span class="pln"> x2 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y1 </span><span class="pun">-</span><span class="pln"> y3</span><span class="pun">)</span><span class="pln"> </span><span class="pun">+</span><span class="pln"> x1 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y3 </span><span class="pun">-</span><span class="pln"> y2</span><span class="pun">))</span><span class="pln"> </span><span class="pun">/</span><span class="pln"> denom<br></br>B </span><span class="pun">=</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x3</span><span class="pun">^</span><span class="lit">2</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y1 </span><span class="pun">-</span><span class="pln"> y2</span><span class="pun">)</span><span class="pln"> </span><span class="pun">+</span><span class="pln"> x2</span><span class="pun">^</span><span class="lit">2</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y3 </span><span class="pun">-</span><span class="pln"> y1</span><span class="pun">)</span><span class="pln"> </span><span class="pun">+</span><span class="pln"> x1</span><span class="pun">^</span><span class="lit">2</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">y2 </span><span class="pun">-</span><span class="pln"> y3</span><span class="pun">))</span><span class="pln"> </span><span class="pun">/</span><span class="pln"> denom<br></br>C </span><span class="pun">=</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x2 </span><span class="pun">*</span><span class="pln"> x3 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x2 </span><span class="pun">-</span><span class="pln"> x3</span><span class="pun">)</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> y1 </span><span class="pun">+</span><span class="pln"> x3 </span><span class="pun">*</span><span class="pln"> x1 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x3 </span><span class="pun">-</span><span class="pln"> x1</span><span class="pun">)</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> y2 </span><span class="pun">+</span><span class="pln"> x1 </span><span class="pun">*</span><span class="pln"> x2 </span><span class="pun">*</span><span class="pln"> </span><span class="pun">(</span><span class="pln">x1 </span><span class="pun">-</span><span class="pln"> x2</span><span class="pun">)</span><span class="pln"> </span><span class="pun">*</span><span class="pln"> y3</span><span class="pun">)</span><span class="pln"> </span><span class="pun">/</span><span class="pln"> denom</span>
with a y = cosh(x) I dont see how you solve that for selected endpoints.
Thats why in the past the chain scripts used a parabola for the shape, it seems easier to find the equations for the curve , finding the tangent at a point etc. .
I will have a look tonight for any catenery equations that might be helpful.
Quote - sorry cage , my maths is just as bad as yours :)
Well, you fake your way through it better than I do, at least. :laugh: I usually assume everyone else knows more than I do. It's safe that way. :lol: And my mathematical ability is disturbingly limited, really. I've only just begun to understand matrices and angles in the past couple of weeks, while working on the loop script.
It seems pretty clear that the y = cosh(x) catenary method, for which I have code, isn't actually adequate. To really be able to apply a catenary, the script would need to be able to handle cases where the chain endpoints are at differing heights.
What about the image and link which lesbentley posted, above? From the image, is Zark applying the catenary correcly, in this case where the chain endpoints are at different heights? It looks like that's just taken the y = cosh(x) curve and stopped before reaching the top of the curve. That seems like a feasible approach, but is it accurate?
If there is more complex math for calculating the catenary when the heights of the endpoints aren't the same, where can that be found? Or does it not exist? 
I'd just like to try to be able to pose a hanging chain in a way that looks nice. :lol: If the solution for the complex catenary cases isn't available, I don't see why using a parabola or mis-applying the simple catenary formula would be objectionable. How many Poser users actually know what a catenary is, anyway? I mean, before reading this thread. :lol: I know I didn't, and I wouldn't have minded having a mathematically inaccurate curve for my hanging chain, if it looked okay.
If the correct solution is available, I'd just like to know what it is, I guess. If it isn't available or is somehow unfeasible, some other approach should be tried.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Attached Link: http://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
> Quote - If there is more complex math for calculating the catenary when the heights of the endpoints aren't the same, where can that be found?You can't solve for a analytically except in a small number of special cases (equal height end points or distance between end points is equal to length of chain), but it is possible to obtain the value by using the equal height solution as a first guess for a "Newton's Method" procedure.
Quote - Or does it not exist?
I never came across an analytical treatment (everything effectively deals with the equal height case).
I was sure that there must be one somewhere, but all I came across was (expensive) programs for calculating the hang of anchor cables for ships and the like.
Quote - What about the image and link which lesbentley posted, above? From the image, is Zark applying the catenary correcly, in this case where the chain endpoints are at different heights? It looks like that's just taken the y = cosh(x) curve and stopped before reaching the top of the curve. That seems like a feasible approach, but is it accurate?
Hanging a bit of cord in front of my monitor, the curve of the Zark chain looks quite close. Now If someone has a fine neck chain they could hang in front of their monitor it would hang more accurately than my cord, which is a bit stiff, and we could know if the Zark curve is correct or not. It certainly looks right to my eye.
I've started doing some simple ERC for the chain, just Side-Side All, Bend All, Twist All, and some dials to stop the chain links from rotating on various axes, which can be handy when posing the chain with the cursor. I'll also try to find a way to make gravity curves, though it won't automatically give you the correct curve, you would have to judge by eye when to stop turning the dial. That's assuming that I can get it to work at all.
Quote - I never came across an analytical treatment (everything effectively deals with the equal height case).
I was sure that there must be one somewhere, but all I came across was (expensive) programs for calculating the hang of anchor cables for ships and the like.
Thanks, nruddock! :thumbupboth: That's helpful. I'll look into the methods of Newton. :laugh:
Quote - I've started doing some simple ERC for the chain, just Side-Side All, Bend All, Twist All, and some dials to stop the chain links from rotating on various axes, which can be handy when posing the chain with the cursor. I'll also try to find a way to make gravity curves, though it won't automatically give you the correct curve, you would have to judge by eye when to stop turning the dial. That's assuming that I can get it to work at all.
Sounds great! I'll hold off on trying to add any ERC until I see what you have. :thumbupboth:
The script is creating the geometry correctly along any of the axes and exporting properly with groups and materials. The .cr2 is being written properly, but without any channels yet. The .cr2 loads correctly into Poser and seems lacking in errors so far. The origins and endpoints are being set correctly, based on the donor .cr2 prepared by lesbentley.
So I just have to put the channels together and add them in to the .cr2. Then any ERC can be plugged in where appropriate.
I doubt I'll get this together tonight, but I think I can finish the basic chain script some time tomorrow, to be posted.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Thanks to lesbentley for working out the template .cr2 which the script uses when setting up the chains. :thumbupboth:
I'll start adding the ERC-handling now. Please let me know if you find any bugs. Basic GUI instructions follow in the next post.
===========================sigline======================================================
Cage can be an opinionated jerk who posts without thinking. He apologizes for this. He's honestly not trying to be a turkeyhead.
Cage had some freebies, compatible with Poser 11 and below. His Python scripts were saved at archive.org, along with the rest of the Morphography site, where they were hosted.
Privacy Notice
This site uses cookies to deliver the best experience. Our own cookies make user accounts and other features possible. Third-party cookies are used to display relevant ads and to analyze how Renderosity is used. By using our site, you acknowledge that you have read and understood our Terms of Service, including our Cookie Policy and our Privacy Policy.












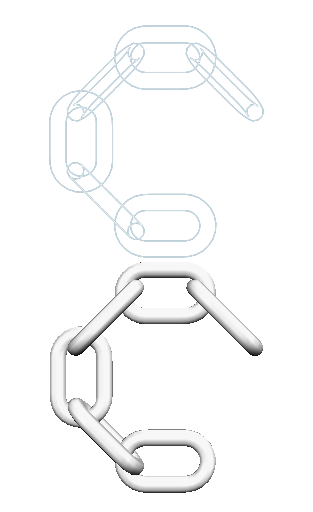
Here is what it looks like with each link rotated 45°. The misplacement of links is an unavoidable consequence of of the origin not being able to be in two places at once. Well perhaps not unavoidable, there might be a way...